2023全国100所名校单元测试示范卷数学卷六第六单元第二次综合测试

2023全国100所名校单元测试示范卷数学卷六第六单元第二次综合测试,我们目前收集并整理关于2023全国100所名校单元测试示范卷数学卷六第六单元第二次综合测试得系列试题及其答案，更多全国100所名校单元测试示范卷试题及答案，请关注微信公众号：考不凡

1、2023全国100所名校单元测试示范卷数学卷二统计必修3

2、2023全国100所名校单元测试示范卷高三数学卷八

3、2023全国100所名校单元测试示范卷英语高三十五

18．已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）过△ABC的两个顶点A，B，且一个焦点为C，另一个焦点D在线段AB上，若|AB|=8，|AC|=6，|BC|=10，直线y=x+m（m为常数）与椭圆交于点M（x₁，y₁），N（x₂，y₂），则x₁x₂的最小值为-12．试题答案

分析 设出椭圆的焦点为C（-c，0），D（c，0），由椭圆的定义可得4a=24，再由直角三角形ADC中，求得CD的长，可得c，进而得到椭圆方程，将直线y=x+m代入椭圆方程，运用韦达定理和判别式大于0，即可得到最小值．

解答 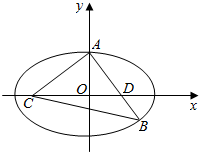解：设椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的两个焦点为C（-c，0），D（c，0），
由椭圆的定义可得|AB|+|AC|+|BC|=4a=24，
解得a=6，由|AC|+|AD|=2a=12，可得|AD|=6，
则直角三角形ADC中，|CD|=6$\sqrt{2}$，
即有c=3$\sqrt{2}$，b=$\sqrt{{a}^{2}-{c}^{2}}$=3$\sqrt{2}$，
即有椭圆方程为$\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{18}$=1，
联立直线y=x+m，可得3x²+4mx+2m²-36=0，
由判别式△=16m²-12（2m²-36）＞0，解得-3$\sqrt{6}$＜m＜3$\sqrt{6}$，
且x₁x₂=$\frac{2{m}^{2}-36}{3}$，当m=0时，取得最小值-12．
故答案为：-12．

点评 本题考查椭圆的定义和方程的运用，考查直线方程和椭圆方程的联立，运用韦达定理和判别式大于0，是解题的关键．