20231全国100所名校单元测试示范卷高三数学卷一

20231全国100所名校单元测试示范卷高三数学卷一,我们目前收集并整理关于20231全国100所名校单元测试示范卷高三数学卷一得系列试题及其答案，更多全国100所名校单元测试示范卷试题及答案，请关注微信公众号：考不凡

1、2023100所名校单元测试示范卷·高三数学十八

2、2023卷临天下《全国100所名校单元测试示范卷》高三数学卷第二单元20. G3DY

3、2023高二全国100所名校单元测试示范卷英语卷二

14．表面积为60π的球面上有四点S，A，B，C，且△ABC是等边三角形，球心O到平面ABC的距离为2，若平面SAB⊥平面ABC，则棱锥S-ABC体积的最大值为$\frac{121\sqrt{3}}{8}$．试题答案

分析 如图，由求得表面积可得球半径OB=$\sqrt{15}$，OD=2可得BD=$\sqrt{11}$，由△ABC是等边三角形可推出AB=$\sqrt{33}$，即△ABC面积为定值，故S在AB的中垂线上且位于平面ABC上方时，棱锥S-ABC体积的最大，过O作平面SAB的垂线段，垂足为H，则HE=OD=2，OH=DE=$\frac{\sqrt{11}}{2}$，SO=$\sqrt{15}$，可求得SH=$\frac{7}{2}$，即棱锥的高最大值为SE=$\frac{11}{2}$．从而可求得棱锥的最大值．

解答 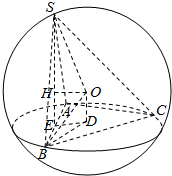解：过O作平面ABC的垂线段OD，垂足为D，过D作DE⊥AB，垂足为E，连接BD，则OD⊥BD，OD⊥DE，
∵4πOB²=60π，∴OB=$\sqrt{15}$，
又∵OD=2，∴BD=$\sqrt{O{B}^{2}-O{D}^{2}}$=$\sqrt{11}$，
∵△ABC是等边三角形，∴D是△ABC的中心，
∴DE=$\frac{1}{2}$BD=$\frac{\sqrt{11}}{2}$，∴AB=2BE=2$\sqrt{B{D}^{2}-A{D}^{2}}$=$\sqrt{33}$．
∴S_△ABC=$\frac{\sqrt{3}}{4}$AB²=$\frac{33\sqrt{3}}{4}$，
由球的对称性可知当S在AB的中垂线上时，S到平面ABC的距离最大，
过O作平面SAB的垂线段SH，垂足为H，
∵平面SAB⊥平面ABC，DE⊥AB，平面SAB∩平面ABC=AB，DE?平面ABC，
∴DE⊥平面SAB，∵SE?平面SAB，∴DE⊥SE，
∴四边形ODEH是矩形，∴OH=DE=$\frac{\sqrt{11}}{2}$，HE=OD=2，
∵OS=OB=$\sqrt{15}$，∴SH=$\sqrt{O{S}^{2}-O{H}^{2}}$=$\frac{7}{2}$，∴SE=SH+HE=$\frac{11}{2}$．
∴V=$\frac{1}{3}$•S_△ABC•SE=$\frac{1}{3}$•$\frac{33\sqrt{3}}{4}$•$\frac{11}{2}$=$\frac{121\sqrt{3}}{8}$．
故答案为$\frac{121\sqrt{3}}{8}$．

点评 本题考察了圆内接几何体的体积，寻找图中的数量关系是本题的难点．