卷临天下2023全国100所名校单元测试示范卷数学卷(四)必修五答案

卷临天下2023全国100所名校单元测试示范卷数学卷(四)必修五答案,我们目前收集并整理关于卷临天下2023全国100所名校单元测试示范卷数学卷(四)必修五答案得系列试题及其答案，更多全国100所名校单元测试示范卷试题及答案，请关注微信公众号：考不凡

1、卷临天下2023全国100所名校单元测试示范卷数学卷(四)

2、卷临天下2023全国100所名校单元测试示范卷高三数学第四单元倒数及其应用答案

3、卷临天下2023年全国100所名校单元测试示范卷高二英语必修五

6．已知平行六面体ABCD-A₁B₁C₁D₁，底面ABCD是边长为1的正方形，AA₁=2，∠A₁AB=∠A₁AD=120°，则异面直线AC₁与A₁D所成角的余弦值为（　　）

试题答案

分析 解：设$\overrightarrow{AB}=\overrightarrow{a}$，$\overrightarrow{BC}$=$\overrightarrow{b}$，$\overrightarrow{C{C}_{1}}$=$\overrightarrow{c}$，则$\overrightarrow{A{C}_{1}}$=$\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}$，$\overrightarrow{{A}_{1}D}$=$\overrightarrow{b}-\overrightarrow{c}$，由此利用向量法能求出异面直线AC₁与A₁D所成角的余弦值．

解答 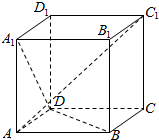解：设$\overrightarrow{AB}=\overrightarrow{a}$，$\overrightarrow{BC}$=$\overrightarrow{b}$，$\overrightarrow{C{C}_{1}}$=$\overrightarrow{c}$，
则$\overrightarrow{A{C}_{1}}$=$\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}$，$\overrightarrow{{A}_{1}D}$=$\overrightarrow{b}-\overrightarrow{c}$，
∵平行六面体ABCD-A₁B₁C₁D₁，底面ABCD是边长为1的正方形，AA₁=2，∠A₁AB=∠A₁AD=120°，
∴$\overrightarrow{A{C}_{1}}•\overrightarrow{{A}_{1}D}$=（$\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}$）•（$\overrightarrow{b}-\overrightarrow{c}$）
=$\overrightarrow{a}•\overrightarrow{b}-\overrightarrow{a}•\overrightarrow{c}+{\overrightarrow{b}}^{2}-\overrightarrow{b}•\overrightarrow{c}+\overrightarrow{b}•\overrightarrow{c}-{\overrightarrow{c}}^{2}$
=1+1-4=-2，
$|\overrightarrow{{A}_{1}D}{|}^{2}$=（$\overrightarrow{b}-\overrightarrow{c}$）²=${\overrightarrow{b}}^{2}+{\overrightarrow{c}}^{2}-2\overrightarrow{b}•\overrightarrow{c}$=1+4+2=7，
|$\overrightarrow{A{C}_{1}}$|²=（$\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}$）²=${\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}+{\overrightarrow{c}}^{2}$-2$\overrightarrow{a}•\overrightarrow{c}$+2$\overrightarrow{a}•\overrightarrow{b}$+2$\overrightarrow{b}•\overrightarrow{c}$
=1+1+4-2-2=2，
∴$|\overrightarrow{{A}_{1}D}|$=$\sqrt{7}$，$|\overrightarrow{A{C}_{1}}|$=$\sqrt{2}$，
∴cos＜$\overrightarrow{A{C}_{1}}，\overrightarrow{{A}_{1}D}$＞=$\frac{\overrightarrow{A{C}_{1}}•\overrightarrow{{A}_{1}D}}{|\overrightarrow{A{C}_{1}}|•|\overrightarrow{{A}_{1}D}|}$=$\frac{-2}{\sqrt{2}×\sqrt{7}}$=-$\frac{\sqrt{14}}{7}$．
∴异面直线AC₁与A₁D所成角的余弦值为$\frac{\sqrt{14}}{7}$．
故选：D．

点评 本题考查异面直线所成角的求法，是基础题，解题时要认真审题，注意向量法的合理运用．